by Marco Taboga, PhD
This lecture discusses some fundamental properties of the expected value operator.
Some of these properties can be proved using the material presented in previous lectures. Others are gathered here for convenience, but can be fully understood only after reading the material presented in subsequent lectures.
It may be a good idea to memorize these properties as they provide essential rules for performing computations that involve the expected value.
Table of contents
Scalar multiplication of a random variable
Sums of random variables
Linear combinations of random variables
Expected value of a constant
Expectation of a product of random variables
Non-linear transformations
Addition of a constant matrix and a matrix with random entries
Multiplication of a constant matrix and a matrix with random entries
Expectation of a positive random variable
Preservation of almost sure inequalities
Solved exercises
Exercise 1
Exercise 2
Exercise 3
Scalar multiplication of a random variable
If is a random variable and
is a constant, then
Proof
This property has been discussed in the lecture on the Expected value. It can be proved in several different ways, for example, by using the transformation theorem or the linearity of the Riemann-Stieltjes integral.
Example Let be a random variable with expectation
and define
Then,
Sums of random variables
If ,
, ...,
are
random variables, then

Proof
See the lecture on the Expected value. The same comments made for the previous property apply.
Example Let and
be two random variables with expected values
and define
Then,
Linear combinations of random variables
If ,
, ...,
are
random variables and
are
constants, then

Proof
This can be trivially obtained by combining the two properties above (scalar multiplication and sum).
Consider as the
entries of a
vector
and
,
, ...,
as the
entries of a
random vector
.
Then, we can also writewhich is a multivariate generalization of the Scalar multiplication property above.
Example Let and
be two random variables with expected values
and define
Then,
Expected value of a constant
A perhaps obvious property is that the expected value of a constant is equal to the constant itself:for any constant
.
Proof
This rule is again a consequence of the fact that the expected value is a Riemann-Stieltjes integral and the latter is linear.
Expectation of a product of random variables
Let and
be two random variables. In general, there is no easy rule or formula for computing the expected value of their product.
However, if and
are statistically independent, then
Proof
See the lecture on statistical independence.
Non-linear transformations
Let be a non-linear function. In general,
However, Jensen's inequality tells us thatif
is convex and
if
is concave.
Example Since is a convex function, we have
Addition of a constant matrix anda matrix with random entries
Let be a
random matrix, that is, a
matrix whose entries are random variables.
If is a
matrix of constants, then
Proof
This is easily proved by applying the linearity properties above to each entry of the random matrix .
Note that a random vector is just a particular instance of a random matrix. So, if is a
random vector and
is a
vector of constants, then
Example Let be a
random vector such that its two entries
and
have expected values
Let
be the following
constant vector:
Define
Then,

Multiplication of a constantmatrix and a matrix with random entries
Let be a
random matrix.
If is a
matrix of constants, then
If is a a
matrix of constants, then
Proof
These are immediate consequences of the linearity properties above.
By iteratively applying these properties, if is a
matrix of constants and
is a a
matrix of constants, we obtain

Example Let be a
random vector such that
where
and
are the two components of
. Let
be the following
matrix of constants:
Define
Then,
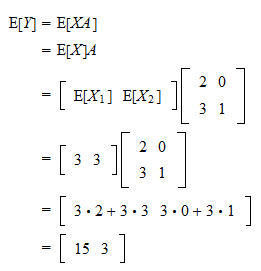
Expectation of a positive random variable
Let be an integrable random variable defined on a sample space
.
Let for all
(i.e.,
is a positive random variable).
Then,
Proof
Intuitively, this is obvious. The expected value of is a weighted average of the values that
can take on. But
can take on only positive values. Therefore, also its expectation must be positive. Formally, the expected value is the Lebesgue integral of
, and
can be approximated to any degree of accuracy by positive simple random variables whose Lebesgue integral is positive. Therefore, also the Lebesgue integral of
must be positive.
Preservation of almost sure inequalities
Let and
be two integrable random variables defined on a sample space
.
Let and
be such that
almost surely. In other words, there exists a zero-probability event
such that

Then,
Proof
Let be a zero-probability event such that
 First, note that
First, note thatwhere
is the indicator of the event
and
is the indicator of the complement of
. As a consequence, we can write
 By the properties of indicators of zero-probability events, we have
By the properties of indicators of zero-probability events, we have Thus, we can write
Now, when
, then
and
. On the contrary, when
, then
and
. Therefore,
for all
(i.e.,
is a positive random variable). Thus, by the previous property (expectation of a positive random variable), we have
which implies
By the linearity of the expected value, we get
Therefore,
Solved exercises
Below you can find some exercises with explained solutions.
Exercise 1
Let and
be two random variables, having expected values:
Compute the expected value of the random variable defined as follows:
Solution
Using the linearity of the expected value operator, we obtain
Exercise 2
Let be a
random vector such that its two entries
and
have expected values
Let be the following
matrix of constants:
Compute the expected value of the random vector defined as follows:
Solution
The linearity property of the expected value applies to the multiplication of a constant matrix and a random vector:
Exercise 3
Let be a
matrix with random entries, such that all its entries have expected value equal to
.
Let be the following
constant vector:
Compute the expected value of the random vector defined as follows:
Solution
The linearity property of the expected value operator applies to the multiplication of a constant vector and a matrix with random entries:
How to cite
Please cite as:
Taboga, Marco (2021). "Properties of the expected value", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/fundamentals-of-probability/expected-value-properties.